第三章-导数与微分
导数
定义:设函数$y = f(x)$在$x_0$的某邻域内有定义,如果极限$\lim\limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim\limits_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x}$存在,则称$f(x)$在点$x_0$处可导,并称此极限值为$f(x)$在点$x_0$处的导数,记为$f’(x_0)$,或$y’|_{x = x_0}$,或$\frac{dy}{dx}|_{x = x_0}$。如果上述极限不存在,则称$f(x)$在点$x_0$处不可导。
【注】常用的导数定义的等价形式:$f’(x_0) = \lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}$,$f’(x_0) = \lim\limits_{h \to 0} \frac{f(x_0 + h) - f(x_0)}{h}$。
定义(左导数):设函数$y = f(x)$在点$x_0$及其某个左邻域内有定义,若左极限$\lim\limits_{\Delta x \to 0^-} \frac{\Delta y}{\Delta x} = \lim\limits_{\Delta x \to 0^-} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = \lim\limits_{x \to x_0^-} \frac{f(x) - f(x_0)}{x - x_0}$存在时,则称该极限值为$f(x)$在点$x_0$处的左导数,记为$f’_-(x_0)$。
定义(右导数):设函数$y = f(x)$在点$x_0$及其某个右邻域内有定义,若右极限$\lim\limits_{\Delta x \to 0^+} \frac{\Delta y}{\Delta x} = \lim\limits_{\Delta x \to 0^+} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = \lim\limits_{x \to x_0^+} \frac{f(x) - f(x_0)}{x - x_0}$存在时,则称该极限值为$f(x)$在点$x_0$处的右导数,记为$f’_+(x_0)$。
导数与左右导数的关系,类比于函数极限与函数左右极限的关系。
定理:
函数$f(x)$在点$x_0$处可导的充分必要条件是它在该点处左导数与右导数都存在且相等。
函数$f(x)$在点$x_0$处可导的必要条件是:$f(x)$在点$x_0$处连续(即$\lim\limits_{x \to x_0} f(x) = f(x_0)$)
定义(区间上可导及导函数):如果$y = f(x)$在开区间$(a,b)$内每一点都可导,则称$f(x)$在区间$(a,b)$内可导。此时对于$(a,b)$内的每一点$x$,都对应一个导数值$f’(x)$,常称$f’(x)$为$f(x)$在$(a,b)$内的导函数,简称为导数。若$f(x)$在区间$(a,b)$内可导,且$f’_+(a)$和$f’_-(b)$都存在,则称$f(x)$在区间$[a,b]$上可导。
导数的左极限:$\lim\limits_{x \to x_0^-} f’(x) = f’_-(x_0) = f’(x_0 - 0)$
导数的右极限:$\lim\limits_{x \to x_0^+} f’(x) = f’_+(x_0) = f’(x_0 + 0)$
导数的左 / 右极限求法:先求导函数;再求导函数在该点的左 / 右极限。
分段函数在分段点的导数一定要用定义来求解!!!可能不可导</span>
导函数的左右极限与左导数、右导数无必然联系
证明:探讨极限$\lim\limits_{h \to 0} \frac{f(x_0 + ah) - f(x_0 - bh)}{ch}$($c \neq 0$)存在时,是否能推出$f(x)$在$x_0$处可导。
若$\lim\limits_{\Delta x \to 0} \frac{f(x_0 + \Delta x) - f(x_0)}{\Delta x} = a$存在,则$f’(x_0) = a$。由此衍生出:
$\lim\limits_{h \to 0} \frac{f(x_0 + ah) - f(x_0)}{ah} = f’(x_0)$(令$\Delta x = ah$);
$\lim\limits_{h \to 0} \frac{f(x_0) - f(x_0 - bh)}{bh} = f’(x_0)$(令$\Delta x = -bh$)。
错误推导分析
若直接将$\lim\limits_{h \to 0} \frac{f(x_0 + ah) - f(x_0 - bh)}{ch}$拆分为:$
\frac{a}{c}\lim\limits_{h \to 0} \frac{f(x_0 + ah) - f(x_0)}{ah} + \frac{b}{c}\lim\limits_{h \to 0} \frac{f(x_0) - f(x_0 - bh)}{bh}
$
进而得到$\frac{a + b}{c}f’(x_0)$存在,就断言$f(x)$在$x_0$处可导,这种推导是错误的。因为拆分后两个单独的极限不一定存在,仅整体极限存在不能保证部分极限存在。
反例验证(以$f(x) = |x|$为例)
取$a = b = c = 1$,$x_0 = 0$,计算:
$
\lim\limits_{h \to 0} \frac{f(0 + h) - f(0 - h)}{h} = \lim\limits_{h \to 0} \frac{|h| - |-h|}{h} = \lim\limits_{h \to 0} \frac{0}{h} = 0
$
此极限存在,但$f(x) = |x|$在$x = 0$处不可导(左导数为$-1$,右导数为$1$,左右导数不相等)。这表明:即使$\lim\limits_{h \to 0} \frac{f(x_0 + ah) - f(x_0 - bh)}{ch}$存在,也不能推出$f(x)$在$x_0$处可导。
结论:极限$\lim\limits_{h \to 0} \frac{f(x_0 + ah) - f(x_0 - bh)}{ch}$存在,不能推出$f(x)$在$x_0$处可导,核心原因是拆分后的两个极限(对应左、右导数相关的极限)不一定存在。
微分
定义(微分):设函数$y = f(x)$在点$x_0$的某一邻域内有定义,如果函数的增量$\Delta y = f(x_0 + \Delta x) - f(x_0)$可以表示为$\Delta y = A\Delta x + o(\Delta x)$($\Delta x \to 0$),其中$A$为不依赖于$\Delta x$的常数,则称函数$f(x)$在点$x_0$处可微,称$A\Delta x$为函数$f(x)$在点$x_0$处相应于自变量增量$\Delta x$的微分,记为$dy = A\Delta x$。
定理:函数$y = f(x)$在点$x_0$处可微的充分必要条件是$f(x)$在点$x_0$处可导,且有$dy = f’(x_0)\Delta x = f’(x_0)dx$。在点$x$处,常记$dy = f’(x)dx$。
导数与微分的几何意义
- 导数的几何意义:
导数$f’(x_0)$在几何上表示曲线$y = f(x)$在点$(x_0,f(x_0))$处切线的斜率。
如果函数$f(x)$在点$x_0$处可导,则曲线$y = f(x)$在点$(x_0,f(x_0))$处必有切线,其切线方程为$y - f(x_0) = f’(x_0)(x - x_0)$。
如果$f’(x_0) \neq 0$,则此曲线$y = f(x)$在点$(x_0,f(x_0))$处的法线方程为$y - f(x_0) = -\frac{1}{f’(x_0)}(x - x_0)$。
如果$f’(x_0) = 0$,则曲线$y = f(x)$在点$(x_0,f(x_0))$处的切线方程为$y = f(x_0)$,即曲线在点$(x_0,f(x_0))$处有水平切线。
【注】 若函数$f(x)$在$x = x_0$处可导,则曲线$y = f(x)$在点$(x_0,f(x_0))$处有切线,反之则不然。例如曲线$y = x^{\frac{1}{3}}$在点$(0,0)$处有切线$x = 0$($y$轴),但函数$f(x) = x^{\frac{1}{3}}$在$x = 0$处不可导($f’(0) = \infty$)。
- 微分的几何意义:
微分$dy = f’(x_0)dx$在几何上表示曲线$y = f(x)$的切线上的增量。
$\Delta y = f(x_0 + \Delta x) - f(x_0)$在几何上表示曲线$y = f(x)$上的增量,且$\Delta y \approx dy$。
连续、可导、可微之间的关系
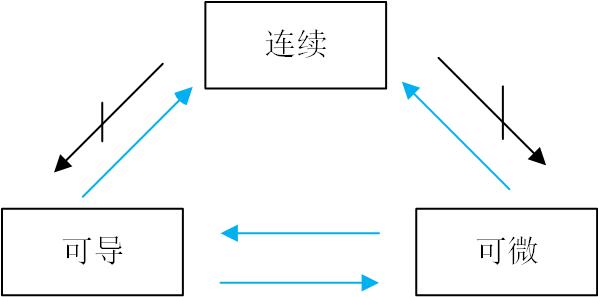
函数可导与可微是等价的;可导(可微)能推出函数连续,但连续不能推出可导(可微)。
若$ f(x) $在$ x_0 $的某领域可导,不能推出$ f’(x) $在$ x_0 $处连续和$ \lim \limits_{x \to x_0} f’(x) $存在。
证明:函数$ f(x)=\begin{cases}x^2\sin\frac{1}{x},&x\neq0\\0,&x = 0\end{cases} $在$ x = 0 $处可导,但$ \lim \limits_{x \to 0} f’(x) $不存在:
解:当$ x\neq0 $时,$ f’(x)=2x\sin\frac{1}{x}-\cos\frac{1}{x} $;当$ x = 0 $时,$ f’(0)=\lim \limits_{x \to 0}\frac{x^2\sin\frac{1}{x}}{x}=0 $。
$ \lim \limits_{x \to 0} f’(x)=\lim \limits_{x \to 0}(2x\sin\frac{1}{x}-\cos\frac{1}{x}) $,无穷小X有界-有界=极限不存在。
二阶可导不保证二阶导数连续或有极限。
总结:若$ f(x)n $阶可导,洛必达法则可对$ f^{n - 1}(x) $,若$ f(x)n $阶连续可导,洛必达法则可对$ f^{n}(x) $使用。
证明可导$ \to $可微:
条件:$ f’(x_0)=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} $。
结论:$ f(x_0+\Delta x)-f(x_0)=A\Delta x + o(\Delta x) $(其中$ A = f’(x_0) $,$ o(\Delta x) $是$ \Delta x $的高阶无穷小)。
因为$ \lim f(x)=A \Leftrightarrow \lim f(x)=A + \alpha $($ \alpha $为无穷小)
所以$ \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}=f’(x_0)+\alpha $($ \alpha $为无穷小)。
进而$ f(x_0+\Delta x)-f(x_0)=f’(x_0)\Delta x+\alpha\cdot\Delta x $,又因为$ \frac{\alpha\cdot\Delta x}{\Delta x}=\alpha $($ \alpha $为无穷小),
所以$ f(x_0+\Delta x)-f(x_0)=A\cdot\Delta x + o(\Delta x) $($ A = f’(x_0) $)。
导数公式及求导法则
1. 基本初等函数的导数公式
$(C)’ = 0$
$(x^{\alpha})’ = \alpha x^{\alpha - 1}$
$(a^{x})’ = a^{x}\ln a$
$(e^{x})’ = e^{x}$
$(\log_{a}x)’ = \frac{1}{x\ln a}$
$(\ln |x|)’ = \frac{1}{x}$
$(\sin x)’ = \cos x$
$(\cos x)’ = -\sin x$
$(\tan x)’ = \sec^{2}x$
$(\cot x)’ = -\csc^{2}x$
$(\sec x)’ = \sec x\tan x$
$(\csc x)’ = -\csc x\cot x$
$(\arcsin x)’ = \frac{1}{\sqrt{1 - x^{2}}}$
$(\arccos x)’ = -\frac{1}{\sqrt{1 - x^{2}}}$
$(\arctan x)’ = \frac{1}{1 + x^{2}}$
$(\text{arccot }x)’ = -\frac{1}{1 + x^{2}}$
($\left[\ln \left(x+\sqrt{x^{2}+1}\right)\right]^{\prime}=\frac{1}{\sqrt{x^{2}+1}}$
$\left[\ln \left(\sqrt{1+x^{2}}\right)\right]^{\prime}=\frac{x}{1+x^{2}}$
2. 求导法则(别忘了后面要加上$dx$)
(1) 有理运算法则
设 $u = u(x)$,$v = v(x)$ 在 $x$ 处可导,则:
$(u \pm v)’ = u’ \pm v’$
$(uv)’ = u’v + uv’$
$\left(\frac{u}{v}\right)’ = \frac{u’v - uv’}{v^{2}} \ (v \neq 0)$
(2) 复合函数求导法
设 $u = \varphi(x)$ 在 $x$ 处可导,$y = f(u)$ 在对应点处可导,则复合函数 $y = f[\varphi(x)]$ 在 $x$ 处可导,且 $\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx} = f’(u)\varphi’(x)$。
(3) 隐函数求导法
隐函数定义:隐函数中,$ y $ 与 $ x $ 的关系隐含在一个等式 $ F(x,y) = 0 $ 中。
例如:$ x^2 + y^2 = 4 $,可变形为 $ x^2 + y^2 - 4 = 0 $。
显函数则是因变量、自变量分别在等式两端,$ y $ 和 $ x $ 各占一边,比如 $ y = 3x $。
求导法则
把 $ y $ 看作与 $ x $ 相关的量,即 $ y = y(x) $,等式两端同时对 $ x $ 求导。
若 $ y $ 对 $ x $ 求导,结果为 $ y’(x) $;
若 $ y^2 $ 对 $ x $ 求导,根据复合函数求导法则,结果为 $ 2y(x) \cdot y’(x) $;
若 $ \ln y $ 对 $ x $ 求导,结果为 $ \frac{1}{y(x)} \cdot y’(x) $。
以 $ x^2 + y^2 = 4 $ 为例,对 $ x $ 求导:
根据求导法则,$ x^2 $ 对 $ x $ 求导得 $ 2x $,$ y^2 $ 对 $ x $ 求导得 $ 2y \cdot y’ $,等式右边 $ 4 $ 对 $ x $ 求导得 $ 0 $,所以有 $ 2x + 2y \cdot y’ = 0 $。
技巧:取对数简化计算,一般应用于指数函数中。
例题1:$ a e^{\arctan\frac{y}{x}} = \sqrt{x^2 + y^2} $($ a>0 $)求 $ y’ $ 。
利用对数运算性质:
$ \ln(ab) = \ln a + \ln b $
$ \ln(a^b) = b\ln a $
$ \ln e^u = u $(因为 $ \ln $ 与 $ e $ 互为反函数)
对原式 $ a e^{\arctan\frac{y}{x}} = \sqrt{x^2 + y^2} $ 两边取自然对数:
$\ln\left(a e^{\arctan\frac{y}{x}}\right) = \ln\left(\sqrt{x^2 + y^2}\right)$
$\ln a + \ln\left(e^{\arctan\frac{y}{x}}\right) = \ln\left((x^2 + y^2)^{\frac{1}{2}}\right)$
$\ln a + \arctan\frac{y}{x} = \frac{1}{2} \ln(x^2 + y^2)$
对等式两边关于 $ x $ 求导:$\left(\arctan\frac{y}{x}\right)’ = \frac{1}{1 + \left(\frac{y}{x}\right)^2} \cdot \left(\frac{y}{x}\right)’$,$\left(\frac{1}{2} \ln(x^2 + y^2)\right)’ = \frac{1}{2} \cdot \frac{1}{x^2 + y^2} \cdot (x^2 + y^2)’$。
$ \frac{1}{1 + \left(\frac{y}{x}\right)^2} \cdot \frac{xy’ - y}{x^2} = \frac{1}{2} \cdot \frac{1}{x^2 + y^2} \cdot (2x + 2y \cdot y’)$
$ \frac{xy’ - y}{x^2 + y^2} = \frac{x + y \cdot y’}{x^2 + y^2}$
$ y’ = \frac{x + y}{x - y}$。
例题2:已知$ f(u) $有二阶导数,且$ f’(0) = 1 $,由$ y - x e^{y - 1} = 1 $确定$ y = y(x) $,设$ z = f(\ln y - \sin x) $,求$ \frac{dz}{dx}\big|_{x = 0} $和$ \frac{d^2z}{dx^2}\big|_{x = 0} $。
步骤 1:求$\frac{dz}{dx}\big|_{x = 0}$
(1)求$ x = 0 $时$ y $的值
将$ x = 0 $代入$ y - x e^{y - 1} = 1 $,可得$ y - 0 = 1 $,即$ y = 1 $。
(2)对$ z = f(\ln y - \sin x) $求一阶导数
根据复合函数求导法则,$ \frac{dz}{dx} = f’(\ln y - \sin x) \cdot (\ln y - \sin x)’ $。
对$ \ln y - \sin x $求导,$ (\ln y)’ = \frac{1}{y} \cdot y’ $,$ (\sin x)’ = \cos x $,所以$ (\ln y - \sin x)’ = \frac{y’}{y} - \cos x $。
因此,$ \frac{dz}{dx} = f’(\ln y - \sin x) \cdot \left( \frac{y’}{y} - \cos x \right) $。
(3)求$ y’ \big|_{x = 0} $
对$ y - x e^{y - 1} = 1 $两边关于$ x $求导:$ y’ - e^{y - 1} - x e^{y - 1} \cdot y’ = 0 $。
将$ x = 0 $,$ y = 1 $代入上式,得$ y’ - e^{0} - 0 = 0 $,即$ y’ = 1 $,所以$ y’ \big|_{x = 0} = 1 $。
(4)计算$ \frac{dz}{dx}\big|_{x = 0} $
将$ x = 0 $,$ y = 1 $,$ y’ \big|_{x = 0} = 1 $代入$ \frac{dz}{dx} $的表达式:$ \frac{dz}{dx}\big|_{x = 0} = f’(\ln 1 - \sin 0) \cdot \left( \frac{1}{1} - \cos 0 \right) = f’(0) \cdot (1 - 1) = 0 $。
步骤 2:求$ \frac{d^2z}{dx^2}\big|_{x = 0} $
(1)对$ \frac{dz}{dx} $求二阶导数
$ \frac{d^2z}{dx^2} = \frac{d}{dx}\left( f’(\ln y - \sin x) \cdot \left( \frac{y’}{y} - \cos x \right) \right) $
根据乘积法则和复合函数求导法则:
$
\begin{align}
\frac{d^2z}{dx^2} &= f’’(\ln y - \sin x) \cdot \left( \frac{y’}{y} - \cos x \right)^2 + f’(\ln y - \sin x) \cdot \left( \frac{y’’ \cdot y - (y’)^2}{y^2} + \sin x \right)
\end{align}
$
(2)求$ y’’ \big|_{x = 0} $
对$ y’ - e^{y - 1} - x e^{y - 1} \cdot y’ = 0 $两边关于$ x $求导:$ y’’ - e^{y - 1} \cdot y’ - e^{y - 1} \cdot y’ - x \left( e^{y - 1} \cdot (y’)^2 + e^{y - 1} \cdot y’’ \right) = 0 $。
将$ x = 0 $,$ y = 1 $,$ y’ = 1 $代入上式,得$ y’’ - 1 - 1 - 0 = 0 $,即$ y’’ = 2 $,所以$ y’’ \big|_{x = 0} = 2 $。
(3)计算$ \frac{d^2z}{dx^2}\big|_{x = 0} $
将$ x = 0 $,$ y = 1 $,$ y’ = 1 $,$ y’’ = 2 $代入$ \frac{d^2z}{dx^2} $的表达式:
$
\begin{align}
\frac{d^2z}{dx^2}\big|_{x = 0} &= f’’(\ln 1 - \sin 0) \cdot \left( \frac{1}{1} - \cos 0 \right)^2 + f’(\ln 1 - \sin 0) \cdot \left( \frac{2 \cdot 1 - 1^2}{1^2} + \sin 0 \right) \\
&= f’’(0) \cdot 0^2 + f’(0) \cdot (1 + 0) \\
&= 0 + 1 \cdot 1 \\
&= 1
\end{align}
$
综上,$ \frac{dz}{dx}\big|_{x = 0} = 0 $,$ \frac{d^2z}{dx^2}\big|_{x = 0} = 1 $。
(4) 反函数求导法
反函数定义:若有函数关系$\begin{cases} f(x) = y \\ g(y) = x \end{cases}$,则$ f(g(y)) = f(x) = y $,且满足$ f(g(x)) = x $,此时$ g $是$ f $的反函数,$ f $也是$ g $的反函数。
导数公式:若$ y = f(x) $在$ x_0 $的某邻域内连续且严格单调,$ y = f(x) $在$ x_0 $可导且$ f’(x_0) \neq 0 $,则其反函数$ x = \varphi(y) $在$ y_0 = f(x_0) $点可导,且有:$ \varphi’(y_0) = \frac{1}{f’(x_0)} $,也可表示为$ [f^{-1}(y)]’ = \frac{1}{f’(x)} $或$ \frac{dx}{dy} = \frac{1}{\frac{dy}{dx}} $。
反函数的导数等于原函数导数的倒数。
例题: 求$ y = \cot x $($ x \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) $)反函数的导数
$ y = \cot x $($ x \in \left(-\frac{\pi}{2}, \frac{\pi}{2}\right) $)的反函数为 $ x = \varphi(y) = \text{arccot } y $。
根据反函数导数公式:若$ y = f(x) $的反函数为$ x = \varphi(y) $,则$ \varphi’(y) = \frac{1}{f’(x)} $。
已知$ (\cot x)’ = -\csc^2 x $,又因为三角恒等式$ \csc^2 x = \cot^2 x + 1 $,且$ y = \cot x $,所以$ \csc^2 x = y^2 + 1 $,则$ (\cot x)’ = - (y^2 + 1) $。
将$ f’(x) = - (y^2 + 1) $代入反函数求导公式,可得:$ \varphi’(y) = \frac{1}{f’(x)} = \frac{1}{- (y^2 + 1)} = -\frac{1}{y^2 + 1} $,即$ (\text{arccot } y)’ = -\frac{1}{y^2 + 1} $。
补充三角函数导数与恒等式(辅助公式)
$ (\cot x)’ = -\csc^2 x $,$ \csc^2 x = \cot^2 x + 1 $;
$ (\tan x)’ = \sec^2 x $,$ \sec^2 x = \tan^2 x + 1 $;
$ \sec x = \frac{1}{\cos x} $,$ \csc x = \frac{1}{\sin x} $。
(5) 参数方程求导法
设 $ y = y(x) $ 是由参数方程 $ \begin{cases} x = \varphi(t) \\ y = \psi(t) \end{cases} $($ \alpha < t < \beta $)确定的函数,则:
一阶导数:若 $ \varphi(t) $ 和 $ \psi(t) $ 都可导,且 $ \varphi’(t) \neq 0 $,则$ \frac{\mathrm{d}y}{\mathrm{d}x} = \frac{\psi’(t)}{\varphi’(t)}$。
二阶导数若: $ \varphi(t) $ 和 $ \psi(t) $ 二阶可导,且 $ \varphi’(t) \neq 0 $,则$\frac{\mathrm{d}^2 y}{\mathrm{d}x^2} = \frac{\mathrm{d}}{\mathrm{d}t}\left( \frac{\psi’(t)}{\varphi’(t)} \right) \cdot \frac{1}{\varphi’(t)} = \frac{\psi’’(t)\varphi’(t) - \varphi’’(t)\psi’(t)}{\varphi’^3(t)}$。
3. 高阶导数
定义(高阶导数):如果 $ y’ = f’(x) $ 作为 $ x $ 的函数在点 $ x $ 可导,则称 $ y’ $ 的导数为 $ y = f(x) $ 的二阶导数,记为 $ y’’ $,或 $ f’’(x) $,或 $ \frac{\mathrm{d}^2 y}{\mathrm{d}x^2} $。
一般地,函数 $ y = f(x) $ 的 $ n $ 阶导数为 $ y^{(n)} = [f^{(n - 1)}(x)]’ $,也可记为 $ f^{(n)}(x) $ 或 $ \frac{\mathrm{d}^n y}{\mathrm{d}x^n} $。即 $ n $ 阶导数就是 $ n - 1 $ 阶导函数的导数,
$f^{(n)}(x_0) = \lim_{\Delta x \to 0} \frac{f^{(n - 1)}(x_0 + \Delta x) - f^{(n - 1)}(x_0)}{\Delta x} = \lim_{x \to x_0} \frac{f^{(n - 1)}(x) - f^{(n - 1)}(x_0)}{x - x_0}.$
【注】:如果函数 $ f(x) $ 在点 $ x $ 处 $ n $ 阶可导,则在点 $ x $ 的某邻域内 $ f(x) $ 必定具有一切低于 $ n $ 阶的导数。
常用的高阶导数公式
- $ (\sin x)^{(n)} = \sin\left(x + n \cdot \frac{\pi}{2}\right) $。
$\sin^{(n)}(ax + b) = a^n \sin\left(ax + b + n \cdot \frac{\pi}{2}\right)$。
$ (\cos x)^{(n)} = \cos\left(x + n \cdot \frac{\pi}{2}\right) $。
- $ (u \pm v)^{(n)} = u^{(n)} \pm v^{(n)} $。
- $ (uv)^{(n)} = \sum_{k = 0}^{n} \mathrm{C}_{n}^{k} u^{(k)} v^{(n - k)} $。注意k从0开始
补充:$\mathrm{C}_{n}^{k}$ 是组合数符号,它表示从 $n$ 个不同元素中取出 $k$ 个元素的组合数。
组合数的计算公式为:$\mathrm{C}_{n}^{k} = \frac{n!}{k!(n - k)!}$,其中 $n!$ 表示 $n$ 的阶乘,即 $n! = n \times (n - 1) \times (n - 2) \times \cdots \times 2 \times 1$,并且规定 $0! = 1$,同时 $k$ 满足 $0 \leq k \leq n$。

